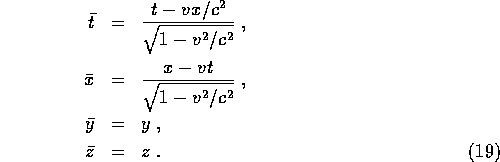Figure 1.5: A simple spacetime diagram
A single point, of fixed x and t is called an event . A particle or observer moving through spacetime maps out a curve x=x(ct), and so represents the position of the particle at different times. This curve is called the particles world- line . The gradient of the world- line is related to the particle's velocity,
so light rays [ v=c ] move on 
lines on this diagram.
Suppose an observer 
uses coordinates ct and x
as in Figure 1.5, and that another observer, with coordinates
and 
, is moving with velocity v
in the x direction relative to . It is clear from
the above discussion that the axis corresponds
to the world- line of 
in the spacetime
diagram of [ see Figure 1.6 ]. We will now use
Einstein's postulates to determine where the axis goes
in this diagram.
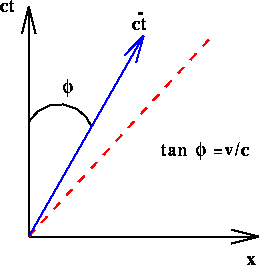
Figure 1.6: The axis of a frame whose velocity is v
relative to .
Consider the following three events in the spacetime diagram
of shown in Figure 1.7 [ A, B and C ] defined
as follows. A light beam is emitted from the point A in
[ event A ]. It is
then reflected at 
[ event B ].
Finally it is received at 
[ event
C ]. How do these three events look in the spacetime diagram
of ?
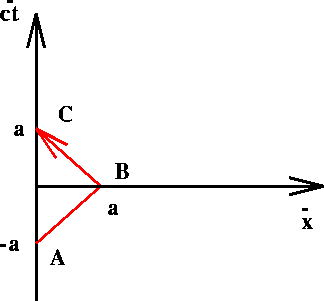
Figure 1.7: Light reflection in
We already know where the axis lies [ see Figure
1.6 ]. Since this line defines 
, we can locate
events A and C [ at 
and 
]. The
second of Einstein's postulate states that light travels with
speed c in all frames. We can therefore draw the same light
beam as before, emitted from A and traveling on a
line in the spacetime diagram of . The reflected beam
must arrive at C, so it is a line with negative
gradient which passes through C. The intersection of these
two lines defines the event of reflection B in . It
follows therefore, that the axis is the line which
passes through this point and the origin [ see Figure 1.8 ].
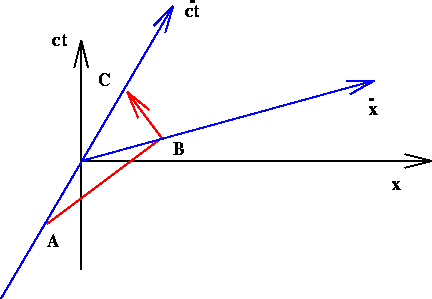
Figure 1.8: Light reflection in as measured by
.
One of the most startling results which follows from this
geometrical construction is that events simultaneous to
are not simultaneous to !
Let us now derive the Lorentz transformations using the geometrical arguments
above and the principle of Special Relativity discussed in the
last section. Assuming that we orient our axes so that
moves with speed v along the positive x axis
relative to , the most general linear transformations we
can write down are
where 
, 
, 
and 
depend only
on the velocity v. Looking at Figure 1.8, we see that
the and axes have the following
equations:
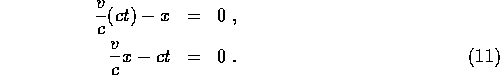
Together with (10), these straight line equations imply
which simplify the first two transformation equations giving
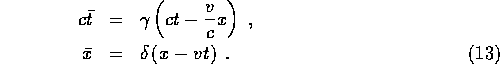
For the speed of light to be the same in both
and we require that
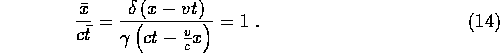
Dividing top and bottom by t gives
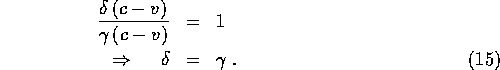
We are therefore left with the following transformation
law for and 
:
The principle of Special Relativity implies that if
, 
,
and 
,
. This gives the inverse transformations
Substituting for and from
(16) in (17) gives,
after some straightforward algebra,
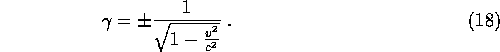
We must choose the positive sign so that when v=0 we get an identity rather than an inversion of the coordinates. The complete Lorentz transformations are therefore,
